疲れて床と同化しながらTLを見ていたら、RTでこんなものがながれてきました。
ポンコツなわっちにこの二つで計測制度に差が出る理由を丁寧目に教えてくれ、桁が増えて情報落ち起こしてるんやろかなぁ?程度にしかわからない pic.twitter.com/FyLe2mqWyX
— フィリア (@philia_wlw) April 23, 2020
こういうのを見ると調べたくなるので、適当に調べてみました。偉そうな単語を使って書いていますが、書いてある内容は暇つぶしレベルです。
目次
1.目的
一般的に小さい順に加減算していくと精度が保たれるといわれている。今回は、上のコードにおいてもそのような状態になった理由を求める。
2.コード
とりあえずツイートのコードを書いた。
3.課題の数学的な解釈
コード内の式を数式にすると、(1)式のようになる。
この数式は次のように変形できる。
最終的にの値は、次のように計算される。
(2)式は の値が小さい順に代入するため、 には大きな値から加算されていく。これがツイートの右側の画像になる。ツイートの左側の画像では、 には小さな値から加算されていきます。これをグラフにすると次のようになる。
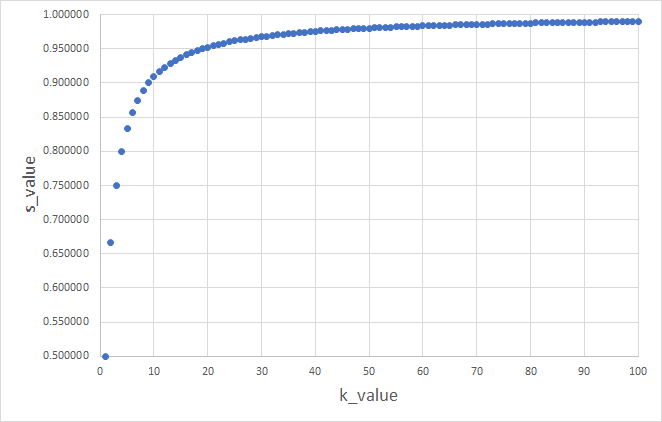
に小さな値から順に加算した場合は次のようになる。
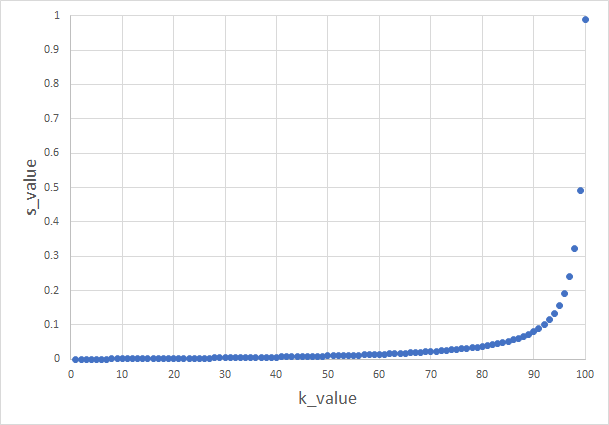
どちらにしろ、(4)式の値に漸近していくはずである。
4.気になったこと
3で書いたように、どう計算しても値は一致するはずである。実際、double型で計算するならば、デフォルトで設定されている有効数字上ではどちらも同じ値を取る。しかし、今回はfloat型であるので精度の問題が発生することは確実である。それがこの課題内容だが、気になった部分があった。
加算していくと値は(4)式の値に漸近するため、 とすれば、 は次第に0に近づくはずである。今回はこの の値を誤差と呼ぶが、グラグ上オーバーシュートしないものと予想していた。
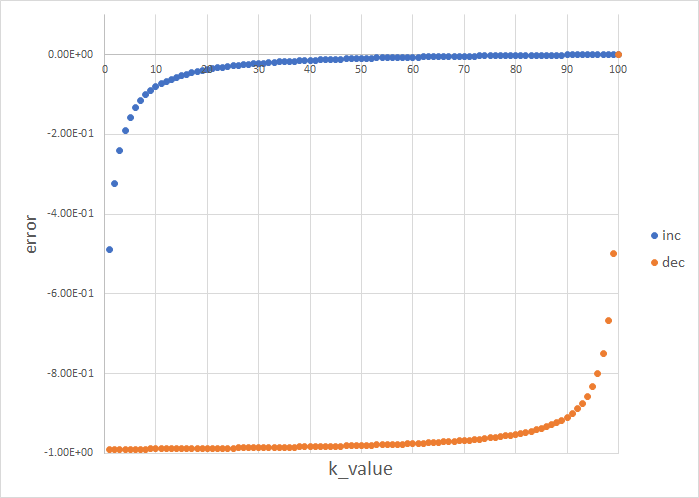
しかし、 にて大きい順に加算する方は誤差が0を超えている。
5.小さい順に加算するほうが精度がよくなる理由?
浮動小数点の加算は指数部を揃えてから計算する。この時、指数が大きい方に合わせる。そして、演算後、仮数部に入り切らなくなった桁に対して四捨五入や切り捨てなどを行う。この時に誤差が生じることになる。
今回の場合は、情報落ち誤差によって誤差が生じているものと考えられる。
情報落ち誤差は大きな数と小さな数の加減算を行った時に、小さい方の値が演算結果に反映されないことによって生じる誤差である。
今回、大きい順に加算した場合このようなことが起こりえる。
最初に0.5という大きな値が加算され、 時点で の値は0.95を超える。このあとはこの大きなsの値に対し、順に小さな値を加算するため情報落ち誤差が発生し続けることになる。
double型と比較した場合、大きい順に加算した時、各kにおいてdouble型sとfloat型sの差の絶対値を取ったグラフがつぎのようになった。また、double型で計算した場合は、同様の計算を行った結果、どの順番に加算しても誤差は0となった。
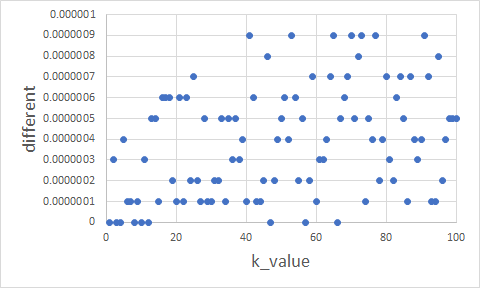
さらに、小さい順に加算する場合、double型で計算したときとfloat型で計算したときの差はつぎのようになった。
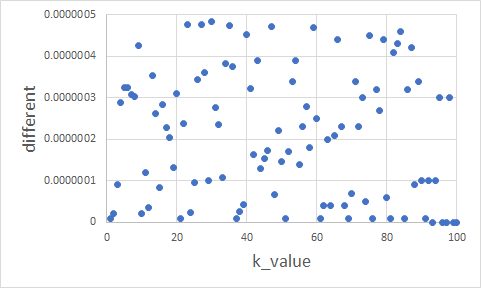
グラフ4とグラフ5を比較すると、グラフ5のほうが差の大きさの幅が小さくなっている。これらから、大きい順に加算した場合は、誤差が大きくなりやすいことが読み取れる。
また、5で初めに述べたように、浮動小数点同士の加減算では指数部が大きい側に合わせて演算することになる。
大きい順で加算した場合、の各値は全て10進数表示で オーダーで表示された。これは、最初にを加算したためである。つまり、その後の全ての加算において に合わせて計算されるため、仮数部の下位ビットには丸め込みが行われ、計算の精度が落ちてしまう。
小さい順で加算した場合は、 の値が10進数表示で次第にオーダーが大きくなるように計算される。これにより、下位ビットの精度がある程度保たれることになる。
6.まとめ
float型を大きい順に加算する場合、情報落ち誤差に注意する必要がある。それを防ぐためには、各値を予想し、できるだけ近い値同士を加算するように演算の順番を考えるべきである。
今回の場合は、小さい順に加算することでの値を次第に大きくすることができるため、次の値を加算する時に情報落ち誤差が小さくすることができる。
また、情報落ち誤差を気にする場合は、よほどのことがない限りdouble型を使うべきである。
7.参考文献
東北大学大学院情報科学研究科 岡谷研究室 計算機工学第3章「実数の表現」
千葉商科大学 商経学部 宮田研究室 コンピュータシステム第三回講義