ここ2週間ABCに参加していなかったのですが、研究室の後輩から質問が来たので、答えるついでにD問題まで解きました。
目次
1.A問題
問題:A – ReLU
キーワード:やるだけ,if文
if文書けますか?という問題。三項演算子の練習にも丁度いいんじゃないですかね?
2.B問題
キーワード:二次元平面,数学
中学校で習う相似ができればわかる問題。ただ単純に中点じゃね?っていうコードを書いたらダメです。
それぞれのy座標から相似比を出して、x座標の差を相似比で分けてあげて、どっちかからその分動かすと答えが出ます。
3.C問題
問題:C – Travel
キーワード:全探索
next_permutationが使えれば解ける問題です。1から出発して1に戻ってくるというのがめんどくさいので、先頭に1を追加、末尾に1を追加して完全なルートを作成しています。
変数を表示させてるあたり、まあまあ苦労してました。原因は27行目のループ回数が2つ多かったことです。
4.D問題
キーワード:いもす法
問題を読めば、1分毎に必要な量がわかれば良さそうだということが読み取れます。つまり、毎分の必要量をタイムラインのようにもち、毎分ごとの必要量と供給可能量を比較してあげればよさそうです。
それを愚直に実装すると次のようになります。
s分からt分までの区間に必要量pリットルを足しています。
しかし、この方法だと、s=0,t=2e5のみの入力があった場合、vector全体をN回も書き込みに行くことになります。どう考えてもTLEになります。
そこで、いもす法と呼ばれるアルゴリズムを用います。競プロでお馴染みの累積和を発展させたアルゴリズムらしいです。
先程の方法では、ある区間を何度も書き込んでいたので低速になりました。ならば、区間の最初と最後に行う演算結果だけを記入しておいて、最後にvector全体で累積和を取れば高速化できます。
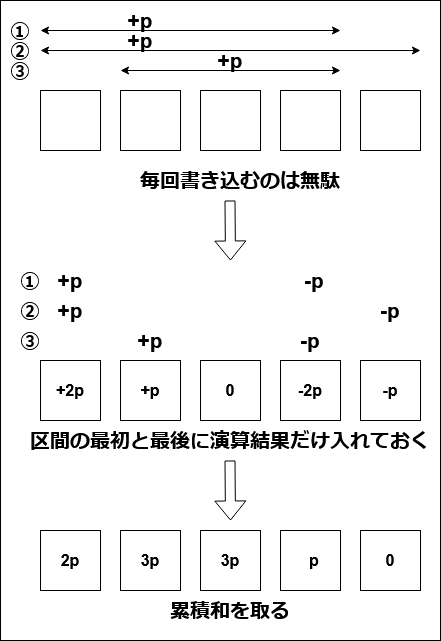
これを実装すると次のようになります。
典型問題らしいので覚えておこうと思います。
5.おわりに
参加していませんが、参加していてもC問題をACしてD問題でTLEしていたと思います。
ただ、競プロ界隈ではいもす法は有名らしいので、こういう典型問題がD問題に出たときはちゃんとACできるように勉強したいと思いました。