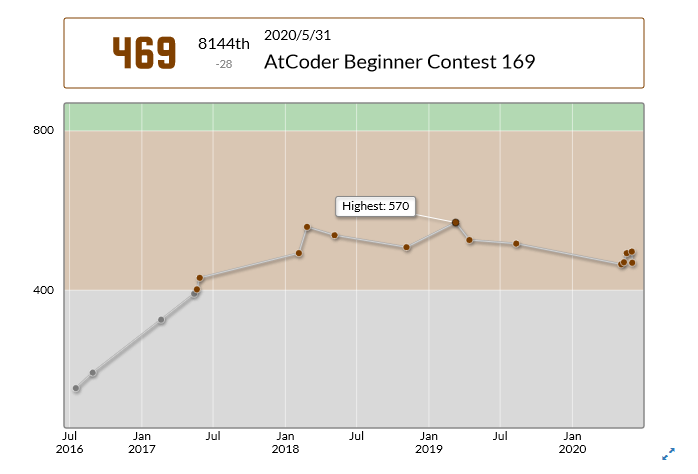
後世に伝説として残るB問題が登場したAtCoder Beginner Contest 169。参加しましたが、Aしか通せなかったのでレーティングが5月頭に戻りました。何一つ成長してねえ・・・。そういうわけで復習と反省を書いていきます。
目次
1.A問題
掛け算の結果を出力するだけ。制約条件も両方とも高々100なので、int型で間に合います。
2.B問題
D問題よりも難しいB問題。このコンテストで最も難しい問題。今までで最も難しいB問題。
今まで最も難しいB問題はTemplate Matchingだと思っていましたが、更新されました。あっちは実装をミスしなきゃ書けるのに対し、こちらはやることはわかっているけどどう実装したらいいかわからない、そういう問題でした。
問題は、N個の整数を掛け合わせた答えを出力せよ、ただし10^18を超える場合は-1と出力せよという問題。
pythonやRustなど桁数を気にしなくても計算できる言語を使えばやるだけ問題です。0が出たときにどう対処するかという問題ぐらいです。
C++で実装する場合はちょっとめんどくさいです。解説動画のチャット欄見てたら、色々出てきたのでそれもメモしていきたいと思います。
2-1.Pythonの場合
Pythonで実装した場合、次のようになりました。
先にリスト内に0がないか確認します。その後、延々に掛け続けて、10-18を超えたら-1を出力して終了します。
私はpythonの文法を完全に忘れていたので、これすら書けませんでした。変数を宣言した時はstring型扱いされるんですね。
2-2.C++の場合
C++で実装した場合、次のようになりました。
0があれば計算しないので配列をソートして、さっさとループを終わらせるようにしています。
それはさておき、重要なのはオーバーフローしたときの処理です。21行目~26行目がそれになります。
if (a[i] <= 1000000000000000000 / ans) {
ans *= a[i];
} else {
flag = false;
break;
}
これは、次の配列の要素を掛けられるかという判定をしています。掛けられるなら答えに掛け、無理なら-1の処理という流れです。
他に見かけた解法としては
- log10を使う
- __int128を使う
- __builtin_mul_overflowを使う
logは誤差が怪しいですが、この問題は通るっぽいです。__int128は解説動画で使ってみてたので、そちらを見てください。
オーバーフローしたか返す関数なんてC++にあったんですね。私が今後これを使う日は来るのだろうか・・・。
void plus( unsigned int x, unsigned int y ) { unsigned int result ; if ( __builtin_add_overflow( x, y, &result ) ) { // オーバーフローした } else { // オーバーフローしなかった } }3つの引数を取り、ひとつ目とふたつ目の引数を加算、減算、乗算したあと、結果をポインターとして取った3つめの引数に書き込む。また、戻り値として、オーバーフローしなかった場合はfalse, オーバーフローした場合はtrueを返す。
ちなみに私は、各数の桁数とそれの余りの積の桁数を取って、18超えたらoutみたいなことを実装していましたが、これをやるならlog10使ったほうが良かったです。どっちにしろ割り算やらで誤差が生じているので、傷口を広げてる実装でした。さすがにそれは提出していなんですが。
また、オーバーフロー判別ですが、掛けた後の値を、先程の掛け算のどちらかの値で割って、もう片方の数になるかどうかで判別できるらしいです。
私はこっちで実装したのですが通りませんでした。さて、これがよくわからないことになっていました。
2-3.オーバーフロー後は未定義動作
次のようなコードを提出したところ、Hand1.txtのみ落ちました。
#include <bits/stdc++.h>
#define rep(i, n) for (int i = 0; i < (n); i++)
#define rep2(i, s, n) for (int i = (s); i < (n); i++)
using namespace std;
using ll = long long;
using P = pair<int, int>;
int main() {
int n;
cin >> n;
ll a[n];
rep(i, n) cin >> a[i];
sort(a, a + n);
ll ans = 1;
rep(i, n) {
if (a[i] == 0) {
ans = 0;
break;
} else {
ll tmp;
tmp = ans * a[i];
if (tmp / ans != a[i] || tmp > 1000000000000000000) {
cout << "-1" << endl;
return 0;
} else {
ans = tmp;
}
}
}
cout << ans << endl;
return 0;
}
落ちたテストケースを試すと、ちゃんと-1と出力されました。そこで、AtCoderのコードテストを通してみたところ0が出力されました。
各変数を出力させてみたところ、この計算をすると、tmpの値が0になります。これはどちらの環境でも同じようです。しかし、この後の挙動が異なります。
家の環境だと、tmp/ans=0となり、掛けた数に一致しないので-1が出力されます。AtCoderのコードテストでは、tmp/ans=ansとなり、hand1.txtは2つの整数があり、その2つが同じ数というものだったので、これは掛けた数に一致し-1を出力します。
その後、掛けた結果が0になるというのはすでに条件分岐で済ませているのだから、tmp=0となった場合は-1とするようにif文を書いたところ、tmpは0でないと判断されて、それでも結局0が出力されました。
おそらく、tmpは内部的には変数同士の掛け算が格納されているためだと思います。これは、tmp/ans=ansとなったところから判断しました。
その後、標準出力すると0にはなるものの、内部的にはans*a[i]を持ち続けているため、-1が出力されずに0が出力されるようになったと考えられます。
このオーバーフロー判別は64ビット整数のオーバーフロー判別についてのメモに"うちでは動く乗算オーバーフロー判定"とあったコードを参考しました。
しかし、これは処理系に依存するようです。また、符号付きのオーバーフローは未定義動作のようです。
そのため、オーバーフローした変数を扱う場合は、自分の環境で動いても、他の環境での動作は保証されません。こういう理由で、私はB問題を通せなかったようです。
まあ、先程参考にしたサイトの下の方に、解説で使われてたオーバーフロー判別が書いてあったんですけどね。オーバーフローを利用するという解法を思いついたのがコンテストの最後で、B通せてない&時間がないで、動いたと言われているコードに飛びついてしまったのも反省点です。ちゃんと記事内を精査しましょう。
3.C問題
情報数学を正しく理解できてるか、という問題らしいです。
掛け算の結果の小数点以下を切り捨てて、結果を整数として出力する問題。
2変数の内、片方は最大10^15の整数、もう片方は整数部が10、小数部が2桁与えられる小数です。
浮動小数点数として掛け算を行うと精度が足りなくなります。これは、doubleの仮数部が52bitであることが原因です。そのため、倍精度浮動小数点数の場合はケチ表現により53bit相当の数を表せるため、表せる桁は2^53は約9*10^15となります。このような理由で、double型の精度は15,16桁と言われるそうです。
さて、今回の場合、整数が最大15桁あり、そこに最大4桁の数をかけ合わせます。こうなると桁数は溢れるため2^-54目で端数処理を行います。これによって起こるのが丸め誤差です。
そこから整数部だけ切り出そうとすると、丸め誤差によって値が正しくなりません。
これを踏まえた上で、ちゃんと処理できるかというのがこの問題です。(多分)
3-1.いろいろな手法
- 小数に100を掛けて演算した後に100で割る
- 小数を文字列として受け取り、小数点を除外した上で整数に変えて演算し、100で割る
どちらにせよ、100掛けて小数を整数にしてから演算をし、最後に100で割っています。これならば整数部においては誤差は精度は保証されるらしいです。
ライブ解説のチャット欄では、1000掛けて1000で割った人や、long double型を使ったらただの掛け算で行けたなどの解法も出ていましたが、これは後でテストケースが追加されて、これらの方法でやった場合は通らなくなっています。
フェネック「ABC169のC問題にafter_contestケースを2つ追加したよー。long doubleで計算してるだけのものと、b*1000.0をしてるものを落とすようなケースになってるから、この2つの方法で通したなら確認してみてねー」
— 競技プログラミングをするフレンズ (@kyopro_friends) May 31, 2020
3-2.自分の解答
コンテスト後にフォロワーさん(というかサークルの大先輩)から文字列として受け取って処理する方法を言われたので、それを実装しました。
3-3.その他
他にもjavaでBigDecimalを使って無理やり実装している人もいました。
4.おわりに
D問題以降はちょっと置いておきます。Aしか通せなかったショックとか眠いとかで無理。
反省点としては、目の前のコードに飛びつかないこと、それを精査すること、そしてC++以外の言語でも問題を解けるようにすること、です。
コードの精査については2-3でも書いたとおりです。もうちょっと下にスクロールしたら処理系に依らない実装方法書いてあったのに。
C++以外の言語でも問題を解けるようにするのは、このコンテストで最も痛感したことです。B問題を見ても分かる通り、Pythonは脳死でゴリ押せます。コンテスト中、私もpythonで書こうとしたのですが、文法をすべて忘れて実装できず。実装できていれば通せたと思います。
別に脳死でゴリ押すためにPythonを使おうというわけでなく、C++では実装がめんどくさいものでも、Pythonなら比較的楽に実装できるというのもあり、そういう恩恵をうまく使ってコンテストを乗り切っていきたいと思ったのです。
今まで解いたAtCoderの問題で、C++437問、Python2問という驚異の割合で解いていますが、これからは練習のためにPythonでも実装するようにしたいと思います。
あとやっぱ今回のコンテストでわかったことは、""小数は闇""。
5.参考文献
AtCoder Beginner Contest 169ライブ配信
64ビット整数のオーバーフロー判定についてのメモ – tomeapp
double演算で保証される精度 – awakia-n's blog
浮動小数点数型と誤差 – 山田 修司プログラミングB(C言語)