連続一様分布、指数分布、正規分布、ガンマ分布の平均と分散の導出

Continuous

前回、離散型確率分布の代表例の平均と分散を計算したので、今回は連続型確率分布の平均と分散です。

扱うのは、連続一様分布、指数分布、正規分布、ガンマ分布です。全部課題の問題です。そのため、指数分布の確率密度関数があまり見ない形になっています。

1.連続一様分布

確率変数 $X$ が次のような確率密度関数を持ちます。

\begin{eqnarray}<br>f(x)=\left\{\begin{array}{ll}<br>\frac{1}{\beta-\alpha} &(\alpha \leq x \leq \beta,\alpha<\beta)\\<br>0 &(上記以外) \\<br>\end{array} \right. \tag{1-1}<br>\end{eqnarray}

平均

\begin{eqnarray}<br>E(X) &=& \int_{-\infty}^\infty xf(x) dx \nonumber \\<br>&=& \int_\alpha^\beta x\frac{1}{\beta-\alpha} dx \nonumber\\<br>&=& \frac{1}{\beta-\alpha}\int_\alpha^\beta xdex \nonumber\\<br>&=& \frac{1}{\beta-\alpha} \left[\frac{x^2}{2}\right]_\alpha^\beta \nonumber\\<br>&=& \frac{\alpha+\beta}{2} \tag{1-2}<br>\end{eqnarray}

分散

分散は $V(X)=E(X^2)-E(X)^2$ で求められます。ここで、 $E(X^2)$ を求めます。

\begin{eqnarray}<br>E(X^2) &=& \int_{-\infty}^\infty x^2f(x) dx \nonumber\\<br>&=& \int_\alpha^\beta x^2f(x)dx \nonumber\\<br>&=& \int_\alpha^\beta x^2\frac{1}{\beta-\alpha}dx \nonumber\\<br>&=& \frac{1}{\beta-\alpha}\int_\alpha^\beta x^2dx \nonumber\\<br>&=& \frac{1}{\beta-\alpha}\left[\frac{x^3}{3}\right]_\alpha^\beta \nonumber\\<br>&=& \frac{1}{\beta-\alpha}\cdot\frac{\beta^3-\alpha^3}{3} \nonumber\\<br>&=& \frac{(\beta-\alpha)(\beta^2+\alpha\beta+\alpha^2)}{3(\beta-\alpha)} \nonumber\\<br>&=& \frac{\beta^2+\alpha\beta+\alpha^2}{3} \tag{1-3}<br>\end{eqnarray}

よって、(1-2)式、(1-3)式より、分散は次のようになります。

\begin{eqnarray*}<br>V(X) &=& E(X^2)-E(X)^2 \\<br>&=& \frac{(\beta-\alpha)^2}{12} \tag{1-4}<br>\end{eqnarray*}

2.指数分布

一般的に指数分布の確率密度関数は次のように表されます。

\begin{equation}<br>f(x) = \left\{\begin{array}{l}<br>\lambda e^{\lambda x} &(0 \leq x \leq \infty,\lambda > 0) \\<br>0 & (-\infty < x < 0) \\<br>\end{array} \right. \tag{2-1}<br>\end{equation}

しかし、今回の課題の確率密度関数は次のようになっています。

\begin{eqnarray}<br>f(x) = \left\{\begin{array}{ll}<br>\frac{1}{\lambda} \exp(-\frac{x-\delta}{\lambda}) &(0 \leq x \leq \infty,\lambda > 0) \\<br>0 & (-\infty < x < 0) \\<br>\end{array} \right. \tag{2-2}<br>\end{eqnarray}

この２つを関数をグラフを描いて比較してみます。まずは、(2-1)式で $\lambda=1$ の時と(2-2)式で $\lambda=1,\delta=1,2$ のときのグラフは下図のようになります。

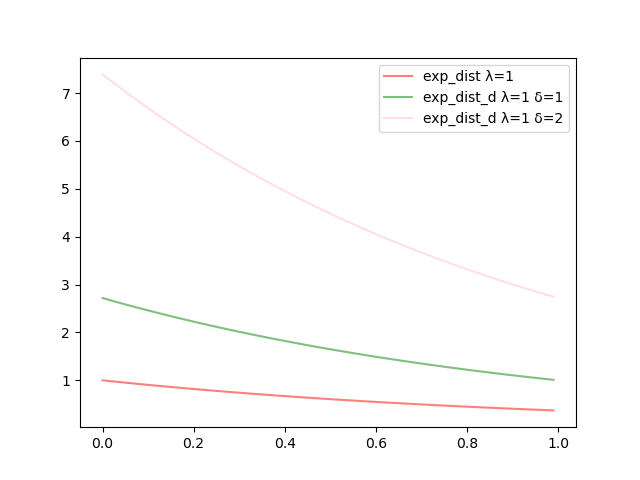
$\lambda=1$ なので、 $\exp$ 部分だけの比較になります。 $\delta$ が大きくなると全体的に上方向へ動いていくことがわかります。

次に、(2-1)式で $\lambda=5$ の時と(2-2)式で $\lambda=5,\delta=0,1,2$ のときのグラフは下図のようになります。

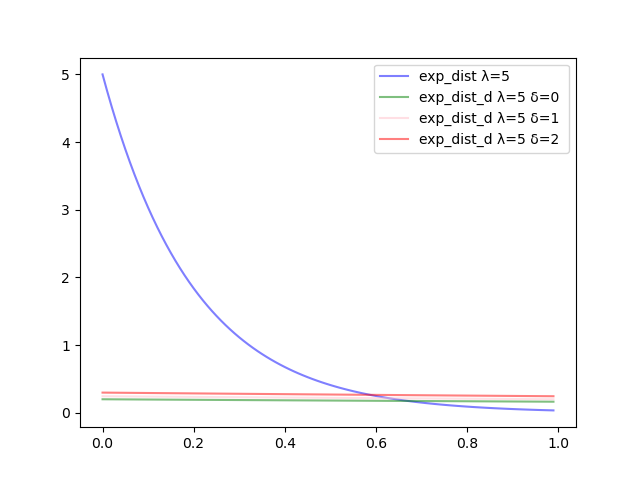
$\lambda$ が大きくなると、(2-2)式は値の変化が(4)式に比べて緩やかになりました。これは $\frac{1}{\lambda}$ による影響です。

さて、今回は(2-2)式の平均と分散を求めることを要求されてたので、(2-2)式に対して計算を行います。

平均

\begin{eqnarray}<br>E(X) &=& \int_{-\infty}^\infty xf(x)dx \nonumber \\<br>&=& \int_\delta^\infty x\frac{1}{\lambda}\exp\left(-\frac{x-\delta}{\lambda}\right) dx \nonumber \\<br>&=& \frac{1}{\lambda}\int_\delta^\infty x \exp\left(-\frac{x-\delta}{\lambda}\right) dx \nonumber \\<br>&=& \frac{1}{\lambda}\int_\delta^\infty x (-\lambda) \left\{\exp\left(-\frac{x-\delta}{\lambda}\right) \right\}' dx \nonumber \\<br>&=& -\int_\delta^\infty x \left\{\exp\left(-\frac{x-\delta}{\lambda}\right) \right\}' dx \nonumber \\<br>&=& -\left\{ \left[x\exp\left(-\frac{x-\delta}{\lambda}\right) \right]_\delta^\infty -\int_\delta^\infty \exp\left(-\frac{x-\delta}{\lambda}\right)dx \right\} \nonumber \\<br>&=& \delta + \left[-\lambda \exp\left(-\frac{x-\delta}{\lambda}\right) \right]_\delta^\infty \nonumber \\<br>&=& \delta + \lambda \tag{2-3}<br>\end{eqnarray}

分散

分散は $V(X)=E(X^2)-E(X)^2$ で求められます。ここで、 $E(X^2)$ を求めます。

\begin{eqnarray}<br>E(X^2) &=& \int_{-\infty}^\infty x^2 \frac{1}{\lambda}\exp\left(-\frac{x-\delta}{\lambda}\right)dx \nonumber \\<br>&=& \int_\delta^\infty x^2 \frac{1}{\lambda}(-\lambda)\left\{ \exp\left(-\frac{x-\delta}{\lambda}\right) \right\}' dx \nonumber \\<br>&=& -\int_\delta^\infty x^2 \left\{ \exp\left(-\frac{x-\delta}{\lambda}\right) \right\}'dx\nonumber \\<br>&=& -\left\{ \left[ x^2 \exp\left(-\frac{x-\delta}{\lambda}\right)\right]_\delta^\infty - \int_\delta^\infty (2x) \exp\left(-\frac{x-\delta}{\lambda}\right)dx \right\} \nonumber \\<br>&=& \delta^2 + 2\lambda\int_\delta^\infty x\frac{1}{\lambda}\exp\left(-\frac{x-\delta}{\lambda}\right)dx \tag{2-4}<br>\end{eqnarray}

ここで(2-4)式の積分部分は平均を求める時と同じなので、(2-3)式より

\begin{eqnarray}<br>E(X^2) &=& \delta^2+2\lambda(\delta+\lambda) \tag{2-5} \\<br>\end{eqnarray}

よって、(2-3)式と(2-5)式より分散 $V(X)$ は、

\begin{eqnarray}<br>V(X) &=& E(X^2) - E(X)^2 \nonumber \\<br>&=& \delta^2+2\lambda(\delta+\lambda)-(\delta+\lambda)^2 \nonumber \\<br>&=& \lambda^2 \tag{2-6}<br>\end{eqnarray}

となります。

3.正規分布

正規分布の確率密度関数は次のような式で表せます。

\begin{eqnarray}<br>f(x)=\frac{1}{\sqrt{2\pi\sigma^2}}\exp\left(-\frac{(x-\mu)^2}{2\sigma^2} \right) & (-\infty < x < \infty,\sigma > 0) \tag{3-1}<br>\end{eqnarray}

平均

\begin{eqnarray}<br>E(X) &=& \int_{-\infty}^\infty xf(x)dx \nonumber \\<br>&=& \int_{-\infty}^\infty (x-\mu+\mu)f(x)dx \nonumber \\<br>&=& \int_{-\infty}^\infty (x-\mu)f(x)dx+\int_{-\infty}^{\infty}\mu f(x)dx \tag{3-2}<br>\end{eqnarray}

ここで、(3-2)式の１つ目の積分を $A$ 、2つ目の積分を $B$ とします。

\begin{eqnarray}<br>A &=& \int_{-\infty}^\infty (x-\mu)\frac{1}{\sqrt{2\pi\sigma^2}}\exp\left(-\frac{(x-\mu^2)}{2\sigma^2} \right)dx \nonumber \\<br>\end{eqnarray}

ここで $y=x-\mu$ とすると、 $\frac{dy}{dx}=1$ より $dy=dx$ であるので、

\begin{eqnarray}<br>A &=& \int_{-infty}^\infty y \frac{1}{\sqrt{2\pi\sigma^2}}exp\left(-\frac{y^2}{2\sigma^2} \right)dy \nonumber \\<br>&=& \frac{1}{\sqrt{2\pi\sigma^2}}\int_{-\infty}^\infty y \exp\left(-\frac{y^2}{2\sigma^2} \right)dy \nonumber\\<br>&=& -\frac{\sigma^2}{\sqrt{2\pi\sigma^2}}\int_{-\infty}^\infty \left(-\frac{y}{\sigma^2}\right) \exp\left(-\frac{y^2}{2\sigma^2} \right)dy \tag{3-3}<br>\end{eqnarray}

と変形できます。さらに、

\begin{eqnarray}<br>\left\{\exp\left(-\frac{y^2}{2\sigma^2} \right)\right\}' &=& \left(-\frac{y^2}{2\sigma^2} \right)'\exp\left(-\frac{y^2}{2\sigma^2} \right) \nonumber \\<br>&=& -\frac{y}{\sigma^2}\exp\left(-\frac{y^2}{\sigma^2} \right) \tag{3-4}<br>\end{eqnarray}

なので、(3-3)式は(3-4)式を用いて次のように書き換えられます。

\begin{eqnarray}<br>A &=& -\frac{\sigma^2}{\sqrt{2\pi\sigma^2}}\int_{-\infty}^\infty \left\{\exp\left(-\frac{y^2}{2\sigma^2} \right)\right\}'dy \tag{3-5}<br>\end{eqnarray}

これを計算すると、

\begin{eqnarray}<br>A &=& -\frac{\sigma^2}{\sqrt{2\pi\sigma^2}}\int_{-\infty}^\infty \left\{\exp\left(-\frac{y^2}{2\sigma^2} \right)\right\}'dy　\nonumber \\<br>&=& -\frac{\sigma^2}{\sqrt{2\pi\sigma^2}} \left[exp\left(-\frac{y^2}{2\sigma^2} \right) \right]_{-\infty}^\infty \nonumber \\<br>&=& 0 \tag{3-6}<br>\end{eqnarray}

となります。

一方 $B$ は、

\begin{eqnarray}<br>B = \mu\int_{-\infty}^\infty f(x)dx<br>\end{eqnarray}

であり、積分部分は確率密度関数を $(-\infty,\infty)$ の区間で積分しています。これは全ての確率の総和と同義なので1となります。

よって、

\begin{eqnarray}<br>B &=& \mu \tag{3-7}<br>\end{eqnarray}

となり、平均は、

\begin{eqnarray}<br>E(X) &=& A + B \nonumber \\<br>&=& \mu \tag{3-8}<br>\end{eqnarray}

となります。

分散

分散は $V(X)=E(X^2)-E(X)^2$ で求められます。ここで、 $E(X^2)$ を求めます。

\begin{eqnarray}<br>E(X^2) &=& \int_{-\infty}^{\infty} x^2f(x)dx \nonumber \\<br>&=& \int_{-\infty}^{\infty} \{(x-\mu)^2+2\mu x-\mu^2\}f(x)dx \nonumber \\<br>&=& \int_{-\infty}^\infty (x-\mu)^2f(x)dx+\int_{-\infty}^\infty 2\mu xf(x)dx+\int_{-\infty}^\infty (-\mu^2)f(x)dx \tag{3-9}<br>\end{eqnarray}

ここで、(3-9)式の1つ目の積分を $A$ 、2つ目の積分を $B$ 、3つ目の積分を $C$ とします。

\begin{eqnarray}<br>A &=& \int_{-\infty}^\infty (x-\mu)^2 \frac{1}{\sqrt{2\pi\sigma^2}}\exp\left(-\frac{(x-\mu)^2}{2\sigma^2} \right)dx \nonumber \\<br>&=& \int_{-\infty}^\infty \frac{(x-\mu)^2}{\sigma}\frac{1}{\sqrt{2\pi}}\exp\left(-\frac{(x-\mu)^2}{2\sigma^2} \right)dx \nonumber \\<br>&=& \int_{-\infty}^{\infty} \sigma \left(\frac{x-\mu}{\sigma} \right)^2 \exp\left(-\frac{1}{2}\left(\frac{x-\mu}{\sigma}\right)^2 \right) \tag{3-10}<br>\end{eqnarray}

ここで $y=\frac{x-\mu}{\sigma}$ とおくと、 $\frac{dy}{dx}=\frac{1}{\sigma}$ より、 $dx=\sigma dy$ ので、

\begin{eqnarray}<br>A &=& \int_{-\infty}^{\infty} \sigma y^2 \frac{1}{\sqrt{2\pi}}\exp\left(-\frac{y^2}{2} \right) \sigma dy \nonumber \\<br>&=& \frac{\sigma^2}{\sqrt{2\pi}}\int_{-\infty}^{\infty} y^2 \exp\left(-\frac{y^2}{2} \right)dy \nonumber \\<br>&=& \frac{\sigma^2}{\sqrt{2\pi}}\int_{-\infty}^{\infty} y^2 \left(-\frac{1}{y}\right)\left(\exp\left(-\frac{y^2}{2} \right) \right)'dy \nonumber \\<br>&=& \frac{\sigma^2}{\sqrt{2\pi}}\int_{-\infty}^{\infty} (-y) \left(\exp\left(-\frac{y^2}{2} \right) \right)'dy \nonumber \\<br>&=& \frac{\sigma^2}{\sqrt{2\pi}}\left\{\left[-y\exp\left(-\frac{y^2}{2} \right) \right]_{-\infty}^\infty - \int_{-\infty}^{\infty} -\exp\left(-\frac{y^2}{2} \right)dy \right\} \nonumber \\<br>&=& \frac{\sigma^2}{\sqrt{2\pi}}\int_{-\infty}^{\infty}\exp\left(-\frac{y^2}{2} \right)dy \tag{3-11}<br>\end{eqnarray}

ここでガウス積分と呼ばれる積分があります。それは次のような式で書かれます。

\begin{eqnarray}<br>I = \int_{-\infty}^{\infty} e^{-ax^2}dx \tag{3-12}<br>\end{eqnarray}

一般的にガウス積分は公式として用いられます。それは次のようなものです。

\begin{eqnarray}<br>\int_{-\infty}^{\infty} e^{-ax^2}dx = \sqrt{\frac{\pi}{a}} \tag{3-13}<br>\end{eqnarray}

(3-11)式を見ると、積分部分がガウス積分の形をしています。よって、ガウス積分の公式が使えて、(3-13)式より、

\begin{eqnarray}<br>A &=& \frac{\sigma^2}{\sqrt{2\pi}}\cdot\sqrt{2\pi} \nonumber \\<br>&=& \sigma^2 \tag{3-14}<br>\end{eqnarray}

となります。

次に $B$ を求めます。

\begin{eqnarray}<br>B &=& 2\mu\int_{-\infty}^{\infty}xf(x)dx　\tag{3-15}<br>\end{eqnarray}

(3-15)式の積部分部分は平均と同じなので、(3-8)式より、

\begin{eqnarray}<br>B &=& 2\mu\cdot\mu \nonumber \\<br>&=& 2\mu^2 \tag{3-16}<br>\end{eqnarray}

最後に $C$ を求めます。

\begin{eqnarray}<br>C = -\mu^2\int_{-\infty}^{\infty} f(x)dx \tag{3-17}<br>\end{eqnarray}

平均を求める時にも述べたように、(3-17)式の積分部分は全確率の総和と同義なので1となります。よって、

\begin{eqnarray}<br>C = -\mu^2 \tag{3-18}<br>\end{eqnarray}

以上より、 $E(X^2)$ は次のようになります。

\begin{eqnarray}<br>E(X^2) &=& A+B+C \nonumber \\<br>&=& \mu^2+\sigma^2 \tag{3-19}<br>\end{eqnarray}

ゆえに、分散 $V(X)$ は、(3-8)式と(3-19)式より

\begin{eqnarray}<br>V(X) = \sigma^2 \tag{3-20}<br>\end{eqnarray}

と求まります。

4.ガウス分布

ガウス分布の確率密度関数は次のような式で表せます。

\begin{equation}<br>f(x) = \left\{\begin{array}{l}<br>\frac{1}{\Gamma(r)\lambda}\left(\frac{x}{\lambda} \right)^{r-1}\exp\left(-\frac{x}{\lambda}\right) &(0 \leq x < \infty,r>0,\lambda > 0) \\<br>0 & (-\infty < x < 0) \\<br>\end{array} \right. \tag{4-1}<br>\end{equation}

ここで、実部が正であるような複素数 $z$ に対してガンマ関数 $\Gamma(z)$ は次のように定義されます。

\begin{eqnarray}<br>\Gamma(z) = \int_0^\infty t^{z-1}e^{-t}dt<br>\end{eqnarray}

また、基本性質の一つに

\begin{eqnarray}<br>\Gamma(n+1) = n!<br>\end{eqnarray}

というものがあります。これを利用すると、次のようなことが言えます。

\begin{eqnarray}<br>\Gamma(n+1) = n \Gamma(n)<br>\end{eqnarray}

この式はガンマ分布の平均・分散を求めるのに使います。以下の導出では断りなしにこの式を用います。

平均

\begin{eqnarray}<br>E(X) &=& \int_{-\infty}^{\infty} xf(x)dx \nonumber \\<br>&=& \int_0^\infty xf(X)dx \nonumber \\<br>&=& \int_0^\infty \frac{x^r}{\Gamma(r)\lambda^r}\exp\left(-\frac{x}{\lambda} \right) dx\nonumber \\<br>&=& \int_0^\infty \frac{r}{\Gamma(r+1)}\frac{\lambda}{\lambda^{r+1}}x^{(r+1)-1}\exp \left(-\frac{x}{\lambda} \right)dx \nonumber \\<br>&=& r\lambda \int_0^\infty \frac{x^{r+1}-1}{\Gamma(r+1)\lambda^{r+1}}\exp\left(-\frac{x}{\lambda} \right) \tag{4-2}<br>\end{eqnarray}

ここで(4-2)式の被積分関数は、(4-1)式の $r$ を $r+1$ と置換したものと一致します。よって、この被積分関数を区間 $[0,\infty)$ で積分することは、全確率の総和を求めることと同義なので、積分の結果は1になります。

よって、(4-2)式は

\begin{eqnarray}<br>E(X) = r\lambda \tag{4-3}<br>\end{eqnarray}

となります。

分散

分散は $V(X)=E(X^2)-E(X)^2$ で求められます。よって、 $E(X^2)$ を求めます。

\begin{eqnarray}<br>E(X^2) &=& \int_{-\infty}^{\infty} x^2f(x)dx \nonumber \\<br>&=& \int_0^\infty x^2 \frac{1}{\Gamma(r)\lambda}\left(\frac{x}{\lambda} \right)^{r-1}\exp\left(-\frac{x}{\lambda}\right)dx \nonumber \\<br>&=& \int_0^\infty \frac{x^{r+1}}{\Gamma(r)\lambda^r}\exp\left(-\frac{x}{\lambda} \right)dx \nonumber \\<br>&=& \int_0^\infty \frac{r(r+1)}{\Gamma(r+2)}\frac{\lambda^2}{\lambda^{r+2}}x^{(r+2)-1}\exp\left(-\frac{x}{\lambda} \right)dx \nonumber \\<br>&=& r(r+1)\lambda^2\int_0^\infty \frac{1}{\Gamma(r+2)\lambda}\left(\frac{x}{\lambda}\right)^{r+1} \exp\left(-\frac{x}{\lambda} \right)dx \tag{4-4}<br>\end{eqnarray}

ここで(4-4)式の被積分関数は、(4-1)式の $r$ を $r+2$ と置換したものと一致します。よって、この被積分関数を区間 $[0,\infty)$ で積分することは、全確率の総和を求めることと同義なので、積分の結果は1になります。

よって、(4-4)式は

\begin{eqnarray}<br>E(X^2) = r(r+1)\lambda^2 \tag{4-5}<br>\end{eqnarray}

となります。以上、(4-3)式と(4-5)式より、分散 $V(X)$ は、

\begin{eqnarray}<br>V(X) &=& r(r+1)\lambda^2-(r\lambda)^2 \nonumber \\<br>&=& r\lambda^2 \tag{4-6}<br>\end{eqnarray}

となります。

5.おわりに

連続型は積分するだけなので離散型より計算が簡単でした。しかし、ガウス積分とかガンマ関数の定義とか性質とか知らなかったので、私は本当に大学を卒業したのか怪しくなってきました。

とりあえず課題に出てきた代表的な分布の平均と分散はこれで全部です。久しぶりにΣ計算とか積分やったので楽しかったです。ひたすら計算用紙と向き合ってると心が落ち着きます。

あとは、今まで出てきた分布の積率母関数を求めよという課題が残ってます。積率母関数ってなんやねんって感じですし、計算がめんどくさそだなあってなってますが、頑張って終わらせたいと思います。ただ、他にも色々課題が出てるので期日的にそっちが優先です。

6.参考文献

連続一様分布の平均・分散の導出(証明)

正規分布の期待値・分散・標準偏差の導出(証明)

部分積分

ガウス積分の公式

ガンマ分布の期待値と分散を密度関数から導出する

LaTeX入門数学記号(等号、不等号、演算子、集合)

連続一様分布、指数分布、正規分布、ガンマ分布の平均と分散の導出

1.連続一様分布

平均

分散

2.指数分布

平均

分散

3.正規分布

平均

分散

4.ガウス分布

平均

分散

5.おわりに

6.参考文献

関連記事

コメントを残すコメントをキャンセル

1.連続一様分布

平均

分散

2.指数分布

平均

分散

3.正規分布

平均

分散

4.ガウス分布

平均

分散

5.おわりに

6.参考文献

関連記事

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル