ABC167復習

ABC167の復習です。解説動画見ながらやっていました。

今回もC問題で躓きました。やりながら「経験値が足りねえ～～」ってなっていたので、頑張って経験値を貯めます。

1.A問題

よゆーと思ってたら30秒ぐらいフリーズした問題です。こういうところが経験値が足りない所以。

やることは単純で、２つの文字列を取って1文字目から比較するだけ。if分とfor文が書ければ解ける。

私は一瞬「find())使うのか？」となりました。substr()も使わなきゃ・・・。

2.B問題

if文が書ければ解けますが、max()を使えばもっと楽に解けたらしい。

3.C問題

私がつまずいた問題です。

ぱっと見てナップサック問題と思った私が悪かった。もっと単純。多分中学生で場合の数やった子なら方針立てれるんじゃないかなってぐらい単純。実装はちょっと工夫がいるようです。

まず、$N$と$M$が高々12というところで違和感を感じます。つまり、全部の通りを計算させたとしても5000通りにも満たないわけです。なので、全部列挙して最小の値採用でよくね？って考えました。ここまではよかった。

次に、"可能な場合は最小値を出力"を見て、なにか有名なアルゴリズムを使うなと思いました。これがいけなかった。

そういうことで私自身の反省終わり。

方針

こういう問題は数が少ないパターンなら中学校でやったはずです。少し応用問題で、10円玉、100円玉、500円玉を使ってどうこう・・・みたいな問題のほうが近い気がします。

何が言いたいかというと、樹形図が書けるということです。使うなら○、使わないなら☓で最初からバーっと書くと樹形図が完成します。あとは、その樹形図の枝ごとに目標に達成できるか判定し、できるなら金額を算出します。

最後に、それぞれの枝から算出された金額の最小値を出せば解けます。

コード

コードはABC167解説動画を見ながら書きました。

新しく知ったことなど

1.repマクロは便利

今までrepマクロは使ったことがなかったのですが、解説動画見てると便利そうなので今度から使おうかなと思ったり。それと、なぜnに括弧がついてるの？と思いましたが、結合順位でバグる可能性があるかららしいです。

競プロのrepマクロで、括弧が使われている理由

2.ビット演算

    rep(s, 1 << n) {  // s=0...0~1...1まで(2進数表示)

これは樹形図でいう、使う場合を1、使わない場合を0としたときの状態を全数列挙する部分です。

repマクロは、n=3ならば000から111までを列挙してくれます。

f (s >> i & 1)

sの最下位ビットに1が立っているか確認する部分です。これで確認できる理由は次のとおりです。

1. sをiビット右シフトさせると、知りたいbitを最下位ビットに持ってくることができる
2. そこに1(0x01)をANDする(ANDはお互いのbitが1なら1、それ以外なら0になる)
3. 最下位bitが1ならばANDされて1になる。そうじゃないならば0になる

聞けばなるほどなってなりますが・・・一応暗号系の研究室所属なのに、bit演算できないは流石にやばい気がしてる。

忘れていたこと

最小値や最大値を出す時、暫定的な答えと計算してきた答えを比較して、逐次更新するという方法。昔は何もせずに書けてたのに、今は・・・。

余談

bti演算を調べていたらbitsetにたどり着きました。その中のcountでなるほどなとなったのが、「値が2の乗数か判定する」ということです。bitsetのcountはその名の通り立ってるbitをカウントするものですが、値を2進数に変換して、全てのbitが立っていれば2の乗数であることがわかる。なるほどなとなりました。

bit演算を知らなければ、for文で値を2で割り続け、割れなくなった時に余りが0ならOK、それ以外ならダメって実装しそうですが、ビット列を扱えればもっと簡単にできるようです。

4.D問題

テレポーターでテレポートし続け、最終的な場所を出力せよという問題。移動回数が$10^{18}$回なのでまともにやると、おねえさんロボになります。

解説では２つの解法を説明してくれていました。

1.周期を考える

制約条件を見ると$N$が高々$2 \times 10^5$なのに対し、移動回数$X$は最高で$10^{18}$です。これからわかることは、道筋は多分ループしているところがあるだろうということ。($N \leq X$の場合はない場合がありますが)

そういうことで、その周期を求めてやればいいだろうということです。

コード

新しく知ったこと

vectorの初期化

vector<int> o(n + 1, -1);

このように書くと、全て-1で初期化されるらしい。

2.ダブリング

別解として紹介された手法。うまいこと作った表を使って最終的な場所を割り出す方法です。

例えば、1→4→2→3→5→2→・・・(2→3→5はループしてる)となる道筋があったとします。ここから、ある場所を始点としてn回辿った先を記述する表を作ります。また、辿った回数は上の数の2倍になるようにします。

辿った回数\始点	1	2	3	4	5
1	4	3	5	2	2
2	2	5	2	3	3
4	5	3	5	2	2

この表は一つ上の段を見ると下の段が書けるようになっています。例えば1から4回辿った場合、1→(2回辿る)→2→(2回辿る)→5というふうに出せます。これを必要な分だけ作ります。

あともう一つ必要なのが、$X$を2進数にします。そうすると、表の辿った回数と対応させることができるからです。例えば、$X=5$だと、$101_{(2)}$となります。これにより、$X=2^2+2^0$ということがわかるので、1が最初の位置だとすれば表より、1→(4回辿る)→5→(1回辿る)→2というように最後の場所が割り出せます。

ダブリング自体はいろいろな場所で使えるらしいので覚えておこうとおもいました。

コード

to[i][j]ですが、これはjから$2^i$先のノードを表します。これによって表ができていきます。一つ上の段を見れば次の段が書けるというのは、

to[i + 1][j] = to[i][to[i][j]]

で表されています。

5.E問題

数学の問題です。5つとかで実験してみると、各$K$に対するパターンというのは一つの数式であらわせることがわかります。色の割り当て方は$M \times (M-1)^{N-X-1}$通り、グループの分け方は${}_{n-1} {C}_x$通りになります。

コード

なんか難しいこと書いてありますが、Atcoderのライブラリを使っています。すごいねこれ。

新しく知ったこと

1.mod 素数

mod = 998244353の値を出力せよと言われています。FFT(高速フーリエ変換)というアルゴリズムを使うらしい。

$\frac{a}{b}$というのがあったとき、$a\times \frac{1}{b}$として計算するといいらしい。この時、フェルマーの小定理$x^{p-1}\equiv 1 \pmod{p}$と

いうものを利用します。両辺を$x$で割って$\frac{x^{p-1}}{x}\equiv\frac{1}{x}\pmod{p}$より、$x^{p-2}\equiv\frac{1}{x} \pmod{p}$となります。これを利用して逆元を求めると早いらしい。

2.繰り返し二乗法

$x^{13}$を求めると、$x$を13回掛けることになります。これを$x^{13}={x^6}^2\cdot x$、$x^6={x^3}^2$というようにやれば計算回数を抑えられます。

6.F問題

括弧列というよくある問題らしいです。このような問題のときは折れ線にするといいらしい。

方針

'('を+1、')'を-1とします。そして各断片をいくつ下るかと増減という2つの情報にします。

解説で挙げてた具体例を使うと、"( ( )"、") ( ( ("、") ) ( ) )"という断片が与えられたとします。これはこの順番に並べると正しい括弧列になるのですが、それぞれを+1と-1にして折れ線にすると次のようになります。

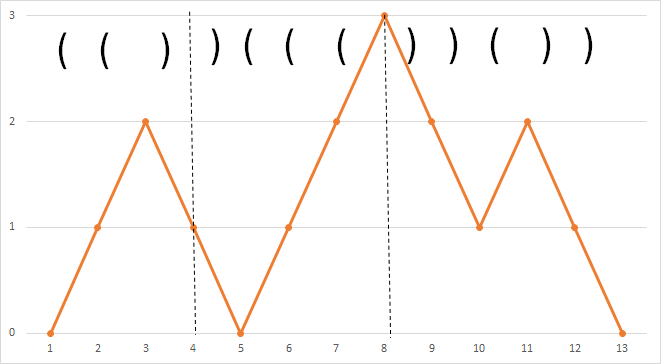
そして、次のように2つの情報を定義します。

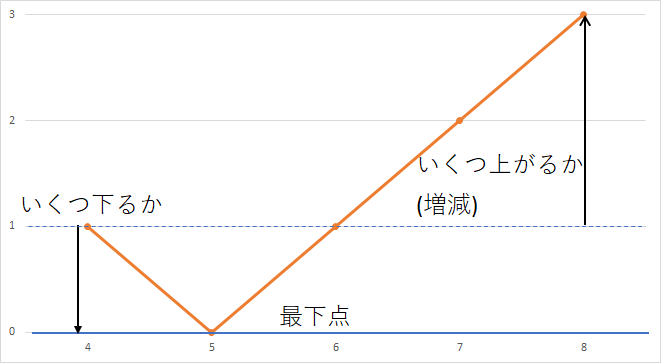
2つの情報を(いくつ下る,増減)というように表せば、先程の断片は(0,1)、(-1,2)、(-3,-3)となります。

次にこの情報を用いて断片を2種類に分けます。どうするかと言うと、増減は高ければ高いほどいいので、増減が正か負かで分類します。

そうすると、断片の結合順番は先に増減が正のものを繋げ、後で増減が負になるものを繋げばいいことがわかります。

ところで、正しい括弧列の条件は

• 0で終わる(増減の総和が0)
• どの部分も0未満にならない

というものです。

さて、先に増減が正のものを繋げますが、正しい括弧列の条件の2番目から、変に繋げると正しくなりません。

そのため、

• 増減が正にものはすぐに繋げて良い
• 最下点(いくつ下るか)が高い順に繋げると良い

ということが言えます。

次に、増減が負のものについて考えますが、これは右側から繋げていくと考えやすくなるらしいです。

つまり、増減が負のものに関しては、右側から見た時の、(いくつ下る,増減)を出すと、増減が正の場合と同じように考えることができます。

コード

新しく知ったこと

1.<bits/stdc++.h>

競プロだと使っている人が多い印象です。競プロ以外だと使わないほうが良いらしいですが。これなんですが、MinGWで入れたgccならそのまま使えます。

2.emplace_back

ぶっちゃけpush_backみたいなものっぽい？しかしぐぐると、emplace_back vs push_backの記事がいっぱい出てきて、なんじゃこりゃってなっています。パフォーマンス的にはemplace_backのほうが無駄がないっぽいですが・・・。

3.rbegin,rend

今回は大きい順にsortするので使ってるようです。これらは、末尾を指すイテレータが返ってきます。コンテナ内を逆向きに走査するときとかに使うらしい。

そういえば、sortならgreater<Type>()使えば降順sortできたなあと思い出しました。

どっち使ってもいいっぽいですが、コードの書きやすさ的にrbegin,rendを使うほうが良さそう。すでに速さの差もないらしい。

4.範囲for

for (char c : s)

とか書かれている部分です。

for ( for-range-declaration : for-range-initializer ) statement

for-range-declarationには変数宣言を書く。ここで宣言した変数に範囲内の要素が先頭から終端まで順番に代入される。 for-range-initializerにはfor文が処理すべき範囲を表す値を書く。

こういう書き方ができるらしい。なんかPythonのfor文みたいですね。

7.おわりに

解説聞くとなるほどなあ～ってなるのですが、コンテスト中はなんじゃこれ！？ってテンパってるクソ雑魚なので、過去問やりつつ勉強したいと思います。

まずはサボってた期間のA,B問題埋めかな。終わったらC問題埋めます。

8.参考文献

AtCoder Beginner Contest 167解説動画

C++日本語リファレンス std::bitset::count

とづんのブログ ビット演算「特定ビットを判定する

C++日本語リファレンス std::vector::コンストラクタ

atcoder-live/library

C++日本語リファレンス std::vector::emplace_back

とにかくあぶなくないRiskのブログ 降順のソート方法

C++日本語リファレンス 範囲for文