C,D,Eの中で一番簡単な問題がE問題と言われる不思議なコンテストでした。私はA,B,Cの3完でした。Dは実装が重い・・・。そういうわけで復習です。
目次
1.A問題
数学Aの問題。
個の"区別できない"お菓子を二人に分ける、ただしどちらも少なくとも1つ貰うとするという問題です。
高校でやりました。さらに最近生徒に教えた気がします。でも1WAしました。
1-1.間を分ける
お菓子を丸で表して一列に並べます。その間に棒を1本差し込みます。この棒の左右に分けた領域内の個数を貰った個数とするという考え方です。
条件が「0個でもよい」という場合は、一列に並べた丸の両端も棒を差し込める場所として考えます。
今回は「少なくとも1個」という条件なので両端に棒を差し込むことはできません。よって、丸の間は丸の個数より1つ少ないので、計算式はとなります。
1-2.1つずつ分け与えたあとで更に分配する
先に1つずつ渡しておくことで、「少なくとも1つ貰う」という条件を、残りのお菓子に対して「貰う個数は0個でもよい」という条件に変える考え方です。
先に2人に1つずつ渡したので、残り個数は個。これを「貰う個数は0個でもよい」という条件で分配する通りの数を考えます。
1-1で書いた両端を含めて間に棒を差し込むという方法もありますし、丸と棒を一列に並べる通りと考えることもできます。どちらにしろ、計算式はとなります。
1-3.実装
わざわざ場合分けしていますが、しなくても大丈夫です。
1-4.WAした理由
区別がある場合の分け方で考えてしまいました。
高校の問題集には「人を2部屋に分ける。どちらの部屋も少なくとも1人を入れる場合、何通りの分け方があるか」という問題と同じです。
しかし、この問題では区別がないため、分けた後の個数が同じ場合があると1通りとして数えます。これでは正しくありません。
2.B問題
B – Palindrome with leading zeros
先頭に0を0個以上付け足して回文数にできるかという問題です。面倒くさそうですがそんなにめんどくさくないです。
まず、与えられる数の先頭に0が来ることは、数が0の時以外ありえません。(当たり前ですが、コンテスト中私が勘違いしていた部分です。)
そして、末尾から初めて0以外の数字が出てくる区間以外は、それ自身で回文数になっていなければいけません。
よって、末尾から初めて0が出てくるまで10で割り続け、残った数が回文数かどうか判別することで答えを得られます。
ただし、与えられた数が0の場合、実装方法によっては無限ループになるので注意しましょう。
2-1.実装
0で無限ループするため、予め処理してプログラムを終了させています。
3.C問題
二次元平面をちょうどRだけ移動して、座標(X,Y)に到達するために必要な最小歩数を求める問題。
考察が難しそうだし、浮動小数点を扱うため誤差でバグりそうと読むだけで嫌な予感がする問題です。
さて、考察ですが入力例2と入力例3の図が役に立ちます。
入力例3では2歩で移動する例が示されています。ここから、距離2R以内の場合、必ず最高で2歩で到達することができることがわかります。また、二本の矢印が成す角をとすると、二本の矢印で作られる三角形のもう一つの辺の長さはになります。
このはなんでもよく、例えば距離0.01を満たすために設定してもよいです。よって、2つの矢印を繋げることで0から2Rの距離を自由に作り出すことができます。
次に入力例2では、R移動した後、二本の矢印で距離を調整しています。
この図から基本的に指定された座標まで距離Rで移動し、距離Rで移動できなくなったら2歩を組みわせて座標へ到達するのがいいということがわかります。
以上から、指定座標まで距離R(1歩)で移動し、残り2R以内になった時、距離Rで移動するとちょうど移動できない時2歩を用いると最小歩数になります。
コンテスト中私は台形を作って考えてましたが、結局同じです。
3-1.実装
+3している理由は、+2は斜め移動分、+1は割り切れなかった場合整数部が1小さくなることを補正するためです。
3-2.double型の余り
整数に対しては%を用いて計算できますが、浮動小数点数に関してはfmod関数を用いる必要があります。
3-3.浮動小数点数を整数部と小数部に分解する
modf関数を使います。第2引数がアドレスであることに注意。
4.D問題
覆面算を解けという問題。
そもそも覆面算って何?となりましたし、問題文の説明を読んでも一切イメージが湧かなかったのでググりました。
覆面算(ふくめんざん)は、0から9の数字がそれぞれに対応する別の記号に置き換えられた計算式を与えられ、どの記号が何の数字に対応しているかを推理し、完全な計算式を導き出すパズルである。
小学校の算数パズルとかでやったような気がします。それのソルバーを作れということらしい。
ここから解説放送を見ながらやっています。
さて、まずは与えられた計算式を計算した後の文字式を計算します。つまり下図のような計算を行います。
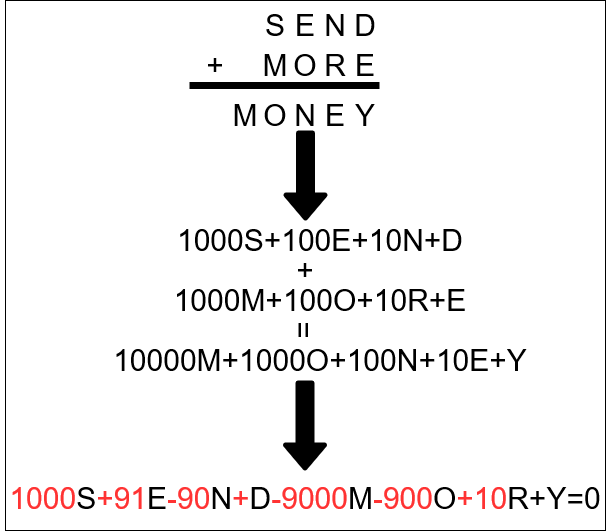
次に、各文字に0~9の数字を割り当てます。ただし、異なる文字に同じ数字を割り当てることはできません。
最終的に、計算結果が0になればそれが解の一つであるため、出力します。
4-1.実装
先頭の文字には0を割り当てられないため、42,43行目のような処理をしています。
このように文字式の係数を予め計算しmapで管理するというのは初めて見たので覚えておこうと思いました。また、10!回の計算は時間内に計算可能だということも合わせて覚えておきたいと思います。
4-2.set
順序付き集合のコンテナクラス。重複した値を保持できない。データの追加、削除、検索の処理速度が高速。格納される要素はそれぞれはキーでもある。
5.E問題
頂点1から各頂点への最短パスに頂点と同じ色の頂点が存在しない時の頂点を全て求めよ、という問題。
深さ優先探索すれば終わるらしい。C,D,Eの中で一番簡単とも言われていました。ただ、実装には深さ優先探索をちゃんと理解している必要があると思います。
5-1.実装
5-2.処理順の例
入力例1を用いて実装したコードがどのように実行されるかを見てみます。
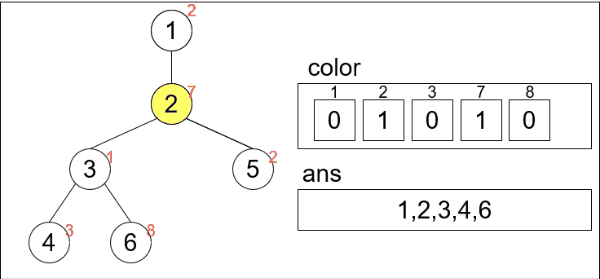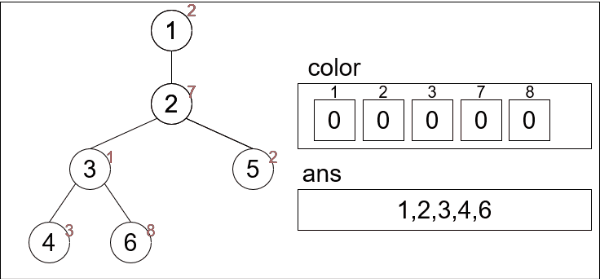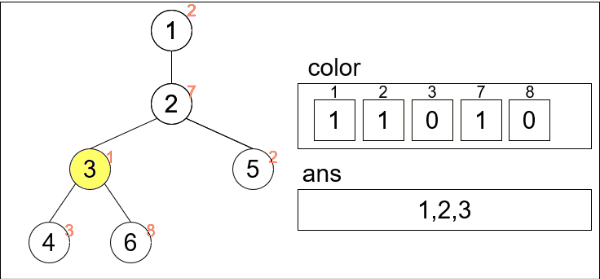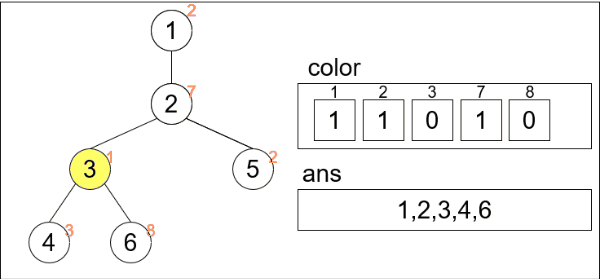
頂点5だけcolor[2]が0でないためansにpush_backされていません。
6.おわりに
過去問やろう。いい加減600台に戻りたい。