前回はバイト先で無限に書類をシュレッダーにぶちこむというクソ仕事のせいで参加できませんでした。ABC177はちゃんと参加できたのと、新しい知識がいくつも出てきたので復習していきます。
また、ABC178が日曜日にありますが、私は石川で友人と呑んだくれる予定なので参加できません。
目次
1.A問題
キーワード:やるだけ,算数
算数ができれば解ける問題です。みはじって懐かしいですよね。
2.B問題
キーワード:文字列,部分文字列,最小値
ある文字列内に指定の文字列を作る場合、最低何箇所書き換えればいいかという問題。私は最初「なにこれ・・・?」となってC問題を先にやってましたが、あとで考えたらやるだけの問題でした。そもそも問題のタイトルがsubstr使えみたいな感じですし。
3.C問題
問題:C – Sum of product of pairs
キーワード:ライブラリ利用,数学
競プロフレンズさんの解説の図がわかりやすいと思います。
フェネック「C問題は ((ΣAi)^2 – Σ(Ai^2))/2 が答えだねー。この問題みたいに、「i<jの全ての組(i,j)について……」って問題で、「全ての組(i,j)について計算してからi=jの分を引いて2で割る」っていうのよく使うテクニックだから覚えておくといいよー」 pic.twitter.com/1stRIjuqj4
— 競技プログラミングをするフレンズ (@kyopro_friends) August 29, 2020
mod計算ですが、自力でmod計算しているとWAになったので、AtCoderの公式ライブラリを用いました。
コードにはありませんが、1億9を表すとき、いつも100000009と書いていたのですが、1e8+9で書けることを知りました。
4.D問題
問題:D – Friends
キーワード:Union-Find,ライブラリ利用
友達同士を同じグループに分けないようにしようという問題。友達関係をグラフでやるとめんどくさいので集合でやって、最も大きい集合のサイズが答えになるというのはわかったのですが、実装の仕方が全くわからずに断念。
集合を作って、さらに集合を結合させたり、どの集合に属しているかを実現するには、Union-FIndというデータ構造があるようです。
Unionが集合をくっつける、Findがどの集合に属しているかを探すことらしく、この2つのクエリを高速に処理できるデータ構造のことのようです。このとき、集合を木構造で保持します。
ここに2つの工夫を行います。それが集合のくっつけ方と経路集約です。
4-1.集合のくっつけ方
まず前提として、各頂点は根にくっつけることとしています。そして、くっつけるときは小さい方の集合を大きい方の集合にくっつけるようにします。こうすることで、木の深さがそれほど深くならずに済みます。こうすると、計算量はO(log(N))になります。これについての証明はABC157の解説放送でやっています。(cf.ABC157解説放送)
4-2.経路集約
根に向かって探索をしますが、深い木だと計算量が多くなるので、同じ根に繋がるならば、その根にくっつけるようにします。
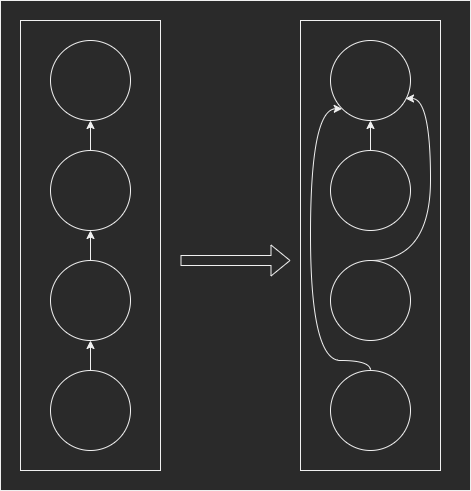
この場合、ならし計算量はO(log(N))となります。
4-3.両方の工夫をする
ならし計算量はO(α(N))になるようです。アッカーマン関数というらしい。
4-4.コード
これは解説放送聞きながらコメントを入れて写経したものです。Union-FIndのコード自体はAtCoderのライブラリにあります。snippetに登録しておきましょう。
4-5.構造体
競プロをやっていると、C問題や簡単なD問題では構造体を使うことがまったくなく、未だによくわかっていません。
構造体とは、いろいろな種類の互いに関連するデータを纏めて、一つの塊にしたものらしいです。この構造体の中には上のコードでも書いたように関数も入れられます。メンバ関数と言うらしいですが。
classとの違いは、デフォルトのアクセシビリティがpublicかprivateからしいです。
5.おわりに
今回はB問題はやるだけの問題なのに通すのが遅れてパフォーマンスを下げてしまいましたが、なんやかんやでレートはプラスになって、highest更新できました。しかし、緑までまだまだ遠いので、アルゴリズムとデータ構造を勉強して行きたいと思います。